Solving linear programming problems in Python with PuLP

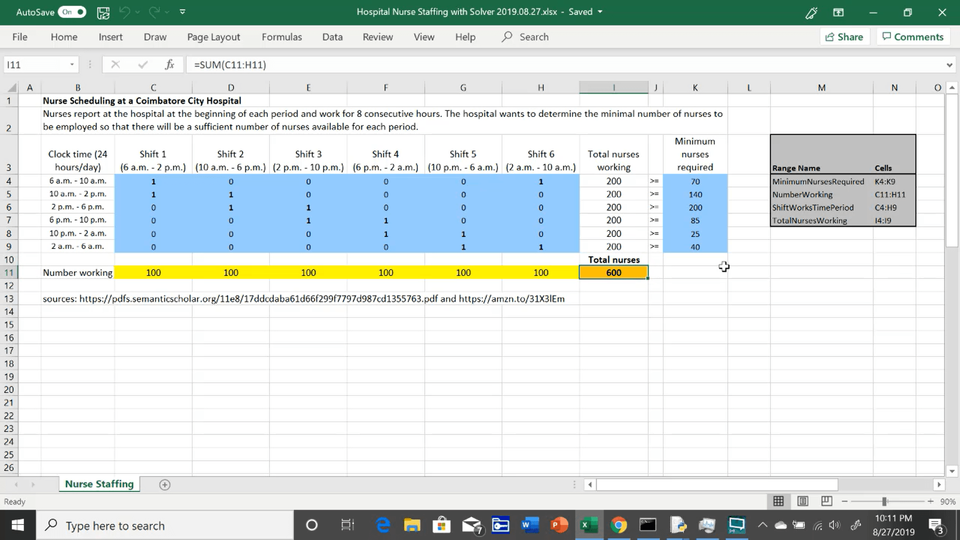
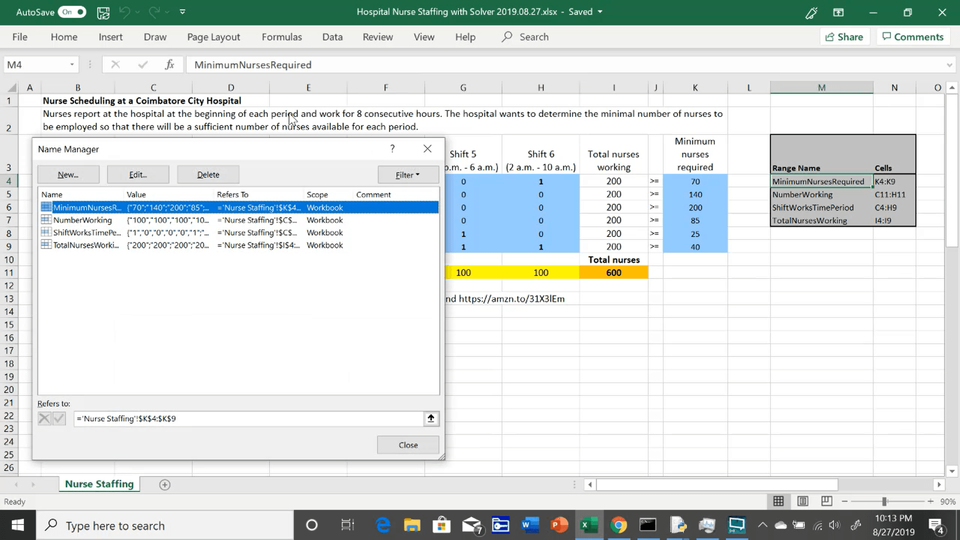
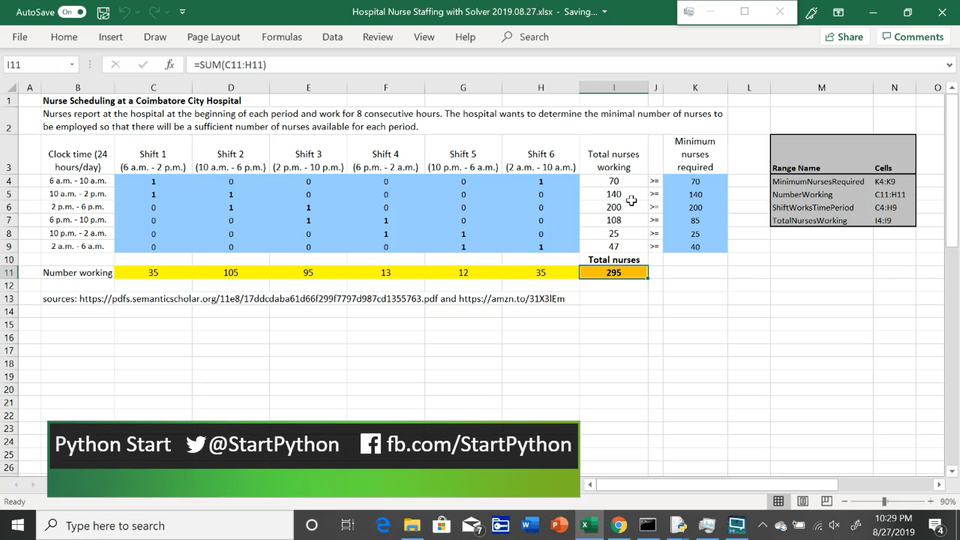
To make this model easier to manage, four named ranges are described in the gray table on the far right:

1. The minimum number of nurses for each 4-hour time window are listed in the right-most blue column
2. The number of nurses needed for each 8-hour shift is shown in the row of yellow cells
3. Definitions of which shifts work each 4-hour time window are defined in the blue cells at C4:H9
4. The total number of nurses working during any given 4-hour time window are shown in column I

These cell ranges are defined and can be viewed in Excel's Name Manager from the "Formulas" Ribbon tab.

This sheet automatically optimizes the schedule using Solver, an Excel add-in. Solver automatically adjusts the default values in the yellow cells to optimize staffing for each 8-hour shift, ensuring adequate staff for each 4-hour window and minimizing the total number of nurses required.

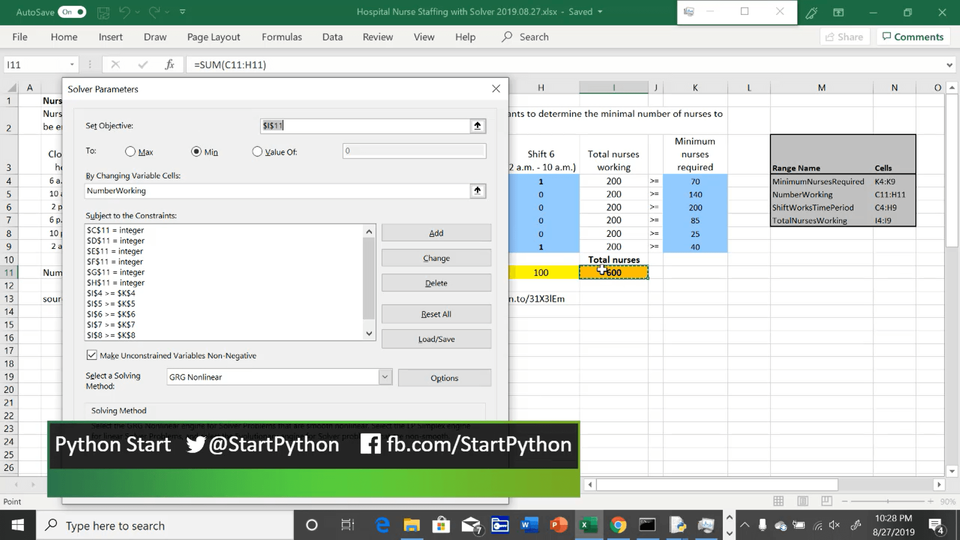
Before we run Solver, notice that our objective is to minimize the total number of nurses required, subject to two types of constraints:

1. The number of nurses must be an integer (whole number) to avoid fractional staffing numbers
2. The number of nurses working in any 4-hour window must be greater than or equal to the minimum

Once all of the Solver parameters are set, Solver is run to find an optimal solution.

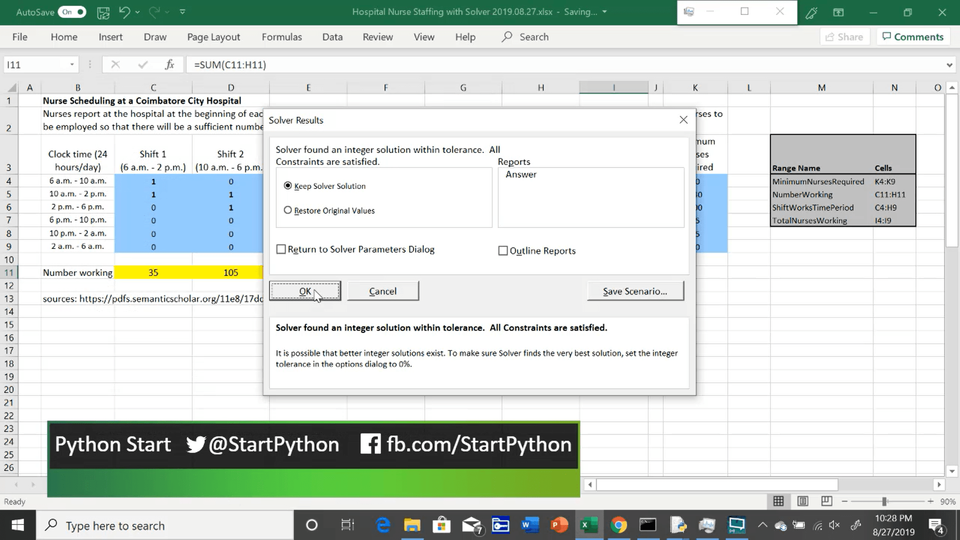
After just a moment, Solver displays a message that indicates that an optimal solution has been found that meets our constraints. Click "OK" and check to be sure the results are accurate.

The resulting schedule meets the staffing constraints for each 4-hour window, while minimizing the total number of nurses required. Now let's take a look at how this can be done in Python using PuLP. The first step is to install PuLP using the command pip install pulp.

Here is some sample code, written in Python, that uses PuLP to solve this linear programming problem. We start by importing the pulp library, then setup a pulp.LpProblem object with a string description and the pulp.LpMinimize parameter to indicate that we want to minimize the number of staff. Next, we create variables to represent the number of nurses working each shift, then define the objective function by adding up the number of nurses for each shift. Finally, we add the six constraints to represent the minimum number of nurses for each 4-hour time window. For example, we need a minimum of 70 nurses for the first 4-hour time window from 6 - 10 a.m.



''' Solving a staffing linear programming problem with PuLP in Python '''

import pulp

prob = pulp.LpProblem("Nurse Staffing", pulp.LpMinimize)

# Variables to represent the number of nurses working each shift

shift1=pulp.LpVariable("Shift1",0,None,pulp.LpInteger)

shift2=pulp.LpVariable("Shift2",0,None,pulp.LpInteger)

shift3=pulp.LpVariable("Shift3",0,None,pulp.LpInteger)

shift4=pulp.LpVariable("Shift4",0,None,pulp.LpInteger)

shift5=pulp.LpVariable("Shift5",0,None,pulp.LpInteger)

shift6=pulp.LpVariable("Shift6",0,None,pulp.LpInteger)

# The objective function is added to 'prob' first

prob += shift1 + shift2 + shift3 + shift4 + shift5 + shift6, "Total Nurses"

# The six constraints to ensure there are enough nurses for each time period

prob += shift6 + shift1 >= 70, "MimimumNurses06amTo10am"

prob += shift1 + shift2 >= 170, "MimimumNurses10amTo2pm"

prob += shift2 + shift3 >= 200, "MimimumNurses02pmTo6pm"

prob += shift3 + shift4 >= 85, "MimimumNurses06pmTo10pm"

prob += shift4 + shift5 >= 25, "MimimumNurses10pmTo2am"

prob += shift5 + shift6 >= 40, "MimimumNurses02amTo06am"

# Solve the problem using PuLP's choice of Solver

prob.solve()

# The status of the solution is printed to the screen

print("Status:", pulp.LpStatus[prob.status])

# Each of the variables is printed with it's resolved optimum value

for v in prob.variables():

  print(v.name, "=", v.varValue)

# The optimized objective function value is printed to the screen

print("Total number of nurses = ", pulp.value(prob.objective))

Now, we are ready to solve using the LpProblem object's solve() method, then print out the results of each variable.

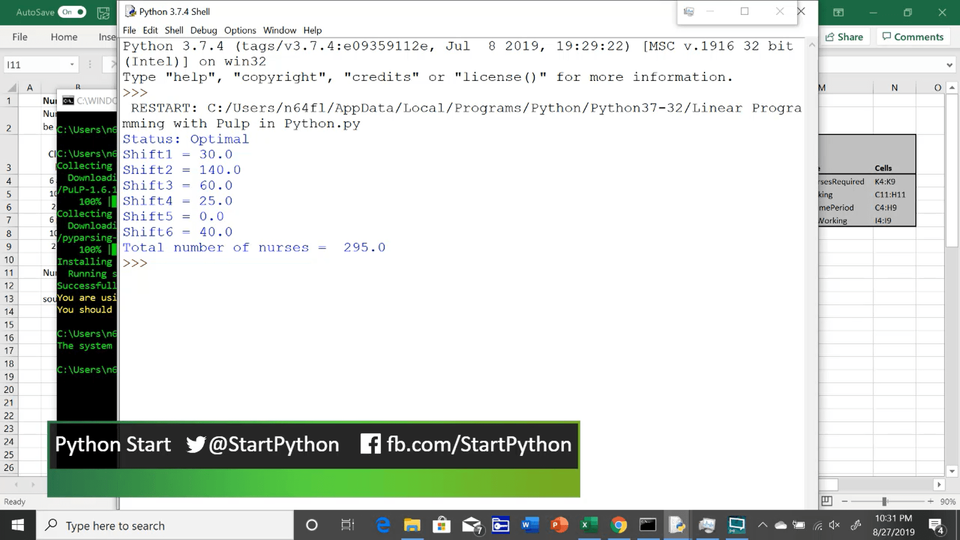
Notice in the output show in figure 7 below that the number of nurses for each shift are different from those we found using Solver in Excel, but each of the constraints is met and the total, minimum number of nurses is the same: 295.



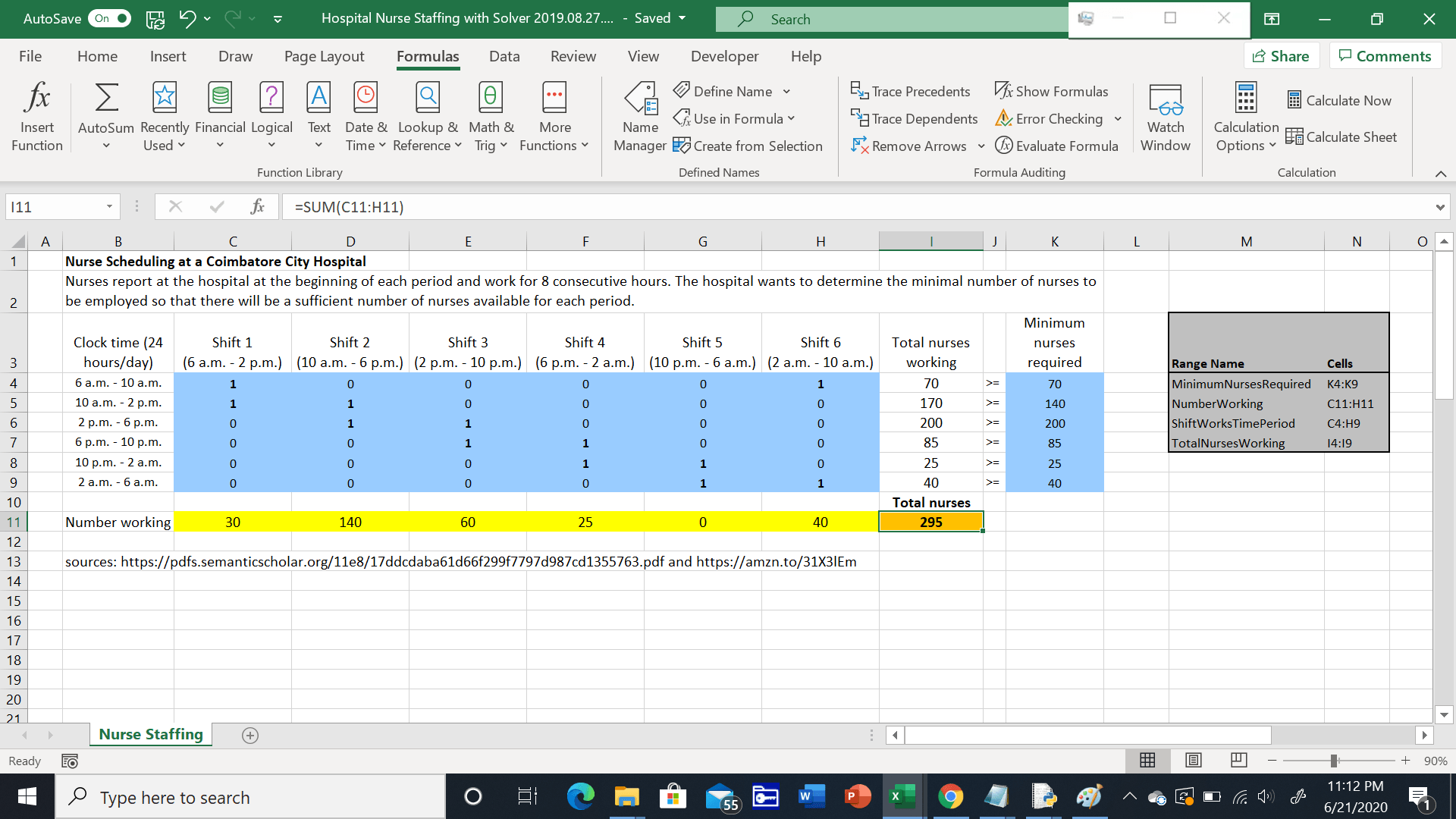
Now we can validate the PuLP results by plugging the shift numbers into our Excel model as shown in Figure 8 below. Even though the 10 p.m. - 6 a.m. shift has 0 nurses, the 25 nurses who started during the previous shift from 6 p.m. - 2 a.m. are sufficient to ensure there are 25 nurses available during from 10 p.m. - 2 a.m.



In this Python example, we have seen how linear programming can help solve real world problems and how these can be solved in Python using PuLP. If you would like to try running this code sample, access it here.

If you have any questions, please leave a comment below or contact us. We look forward to seeing how you use linear programming in Python to solve your real world challenges.